フィルタの離散化について
こちらの記事「ローパスフィルタについて」 でローパスフィルタの連続モデルについての話をしました。
ここでは、フィルタの離散化について記載します。
制御の実機に向けたシミュレーションによる検討、ソフト実装をするためには、連続モデルの伝達関数は離散領域で考える必要があります。 どんな形の伝達関数であれ、sをzに置き換えて最後に時間領域に戻すことで、ソフトウェアなどの実装に利用できますね。
最初にs領域からz領域の変換式を示し、ローパスフィルタとハイパスフィルタを例に離散化を示します。
s領域とz領域について
z領域とs領域の関係は以下となります。$T$はサンプリング時間です。
$$
\begin{align}
z &= e^{Ts}\\
s &=\frac{1}{T}\ln (z)
\end{align}
$$
s領域の伝達関数は、上式を利用してz領域の離散式に変換できます。ただし、ln(z)は計算できないため、近似式を適用する必要があります。$0 < z < 2$ の条件を満たすとき、テイラー展開でき、以下式が得られます。このテイラー展開についてはこちらを参照。
$$
\begin{align}
\ln (z) &= \frac{(z-1)^1}{1}-\frac{(z-1)^2}{2}+\frac{(z-1)^3}{3}-\frac{(z-1)^4}{4}+…\\
\end{align}
$$
1次のみ取り出すと、オイラー近似(前進差分)となります。
$$
s \approx \frac{z-1}{T}
$$
後退差分の場合
$$
s \approx \frac{1-z^{-1}}{T}
$$
逆双曲線関数を利用した近似式の展開もあります。
$$
\begin{align}
\ln (z) &= 2 \tanh^{-1} \frac{z-1}{z+1}\\
&= 2\left(\frac{z-1}{z+1}+\frac{1}{3}\left(\frac{z-1}{z+1}\right)^3
+ \frac{1}{5}\left(\frac{z-1}{z+1}\right)^5 +…
\right)
\end{align}
$$
1次のみ取り出すと、双一次変換双一次変換となります。
$$
s \approx \frac{2}{T}\frac{z-1}{z+1}
$$
ローパスフィルタの離散化(前進差分)
ローパスフィルタの伝達関数
$$
\begin{align}
\frac{Y(s)}{X(s)} &= \frac{1}{T_{c}s+1}\\
\end{align}
$$
前進差分の$s$を代入してみます。
$$
\begin{align}
\frac{Y(z)}{X(z)} &= \frac{1}{T_{c}\frac{z-1}{T}+1}\\
Y(z)\left(T_{c}\frac{z-1}{T}+1\right) &= X(z)\\
\frac{T_c}{T}Y(z)z+(\frac{T-T_{c}}{T})Y(z) &= X(z)\\
Y(z) &= \frac{1}{T_{c}}\left((T{c}-T)Y(z)z^{-1} + TX(z)z^{-1}\right)
\end{align}
$$
時間領域では
$$
y_{n} = \frac{1}{T_{c}}\left((T{c}-T)y_{n-1} + Tx_{n-1}\right)
$$
シミュレーション
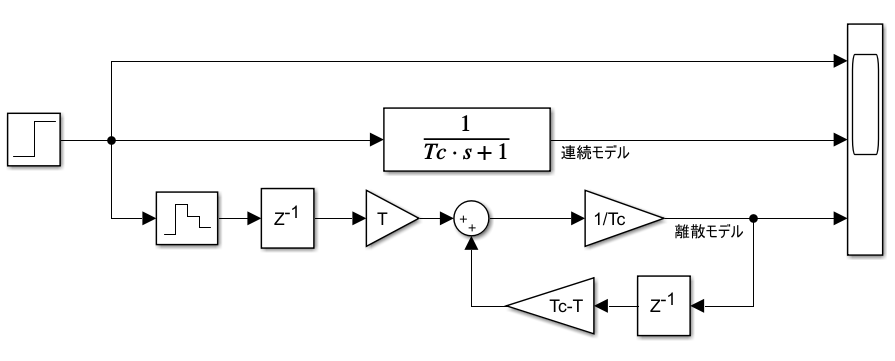
simulinkで連続モデルと離散モデル(前進差分)の比較をしてみます。以下がモデルです。
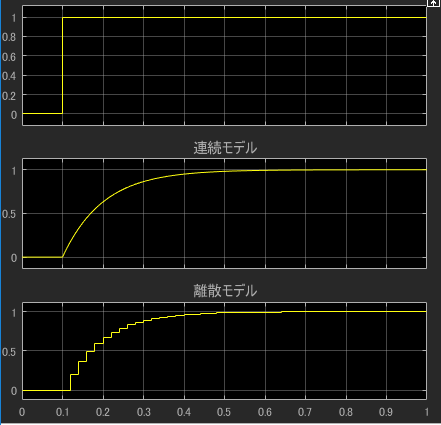
離散モデルを$T=0.02sec$で離散化し、$T_{c}=0.1sec$として、ステップ応答を確認してみます。
サンプリング時間が荒いため、離散モデルはカクカクしてますが、連続モデルと同様な波形になっていることを 確認できます。