はじめに

　繰り返し学習制御は、繰り返し行われる動作の精度改善や周期性のある外乱を抑制するのに効果を発揮するトラッキング制御です。 例えば、繰り返し同じ行動をするロボットアーム追従の制御精度改善やモータの外乱トルクリプル抑制などに利用されているらしいです。

　Simulinkでモータの簡単なモデルを使って、PI制御と組み合わせたILC制御の活用例を紹介してみます。

ILC制御の概要説明

外乱$d_{k}$に対するプロセスを考えてみます。 $$y_{k} = fu_{k}+d_{k}$$ $y_{k}$はシステムの出力、fはプラントの特性、$d_{k}$を外乱としてます。

$$u_{k+1} = u_{k}+\Phi e_{k+1}+\Gamma\int e_{k+1}dt$$

PI制御におけるILC制御誤差は

$$ \begin{align} e_{k+1} &= y_{ref}-y_{k+1}\\
&= e_{k}+y_{k} - fu_{k+1} -d_{k+1}\\
&= e_{k}+y_{k} - f(u_{k}+\Phi e_{k+1}+\Gamma\int e_{k+1}dt) -d_{k+1}\\
&= e_{k}-f(\Phi e_{k+1}+\Gamma\int e_{k+1}dt) + d_{k}-d_{k+1}\\
\end{align} $$

$d_{k}-d_{k+1}$が打ち消しあって、PI制御において周期外乱が消去できます。 kは繰り返しに対する添え字になっており、外乱の周期に対応しています。（離散化の意味ではないことに注意） $y_{ref}$は指令なので、$y_{ref} = e_{k}+y_{k}$(フィードバック)となります。

ここで、周期性を持たない要素に対しては徐々に積算されていくため、制御的にはよくないですね。 そこで、忘却要素をPI制御型のILCに導入します。

$$u_{k+1} = (1-\alpha) u_{k}+\Phi e_{k+1}+\Gamma\int e_{k+1}dt$$ $\alpha$は忘却要素です。上の式より

$$e_{k+1} = (1-\alpha)e_{k}-f(\Phi e_{k+1}+\Gamma\int e_{k+1}dt) +\alpha y_{ref}+ (1-\alpha)d_{k}-d_{k+1}$$

$\alpha$は1より小さい値を設定すると、$(1-\alpha)e_{k}$により、 誤差を減衰させる効果があることがわかります。ただし、$\alpha d_{k}$ となるため、周期性外乱を抑える効果が弱くなります。

シミュレーションモデル

　ILC制御に入る前に、簡単なSimulinkモデルを作成しました。左から、速度指令のステップ入力、PI制御器でq軸電流指令生成します。 本来は電流フィードバックを利用しますが、速度制御器より十分早いとして、ゲイン1.0として省略しました。機械側は 単純にイナーシャ$J_{m}$と摩擦$B_{m}$の簡易モデルとしてます。

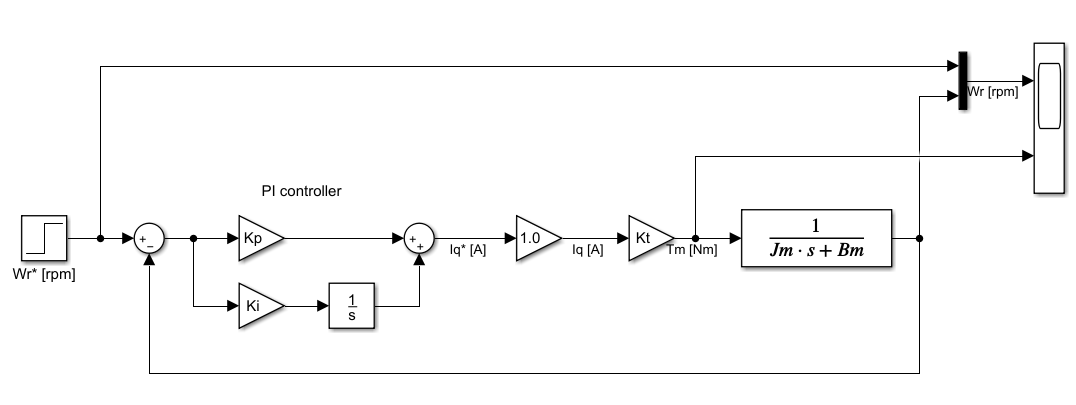
　ILCの話とは関係ないですが、PI制御器の基本的なゲイン設計指針についてメモしておきます。上図のフィードバックの伝達関数 を求めると、 $$ \begin{align} (X(s)-Y(s))(K_{p}+\frac{K_{i}}{s})K_{t}\frac{1}{sJ_{m}+B_{m}} = Y(s)\\
\frac{Y(s)}{X(s)}=\frac{(K_{p}+\frac{K_{i}}{s})K_{t}\frac{1}{sJ_{m}+B_{m}}}{(1+(K_{p}+\frac{K_{i}}{s})K_{t}\frac{1}{sJ_{m}+B_{m}})}) \\
=\frac{(K_{p}+\frac{K_{i}}{s})K_{t}}{(sJ_{m}+B_{m}+(K_{p}+\frac{K_{i}}{s})K_{t})}\\
=\frac{sK_{p}K_{t}+K_{i}K_{t}}{(s^2J_{m}+s(B_{m}+K_{p}K_{t})+K_{i}K_{t})}\\
\end{align} $$

ここで、第1項は2次系のバンドパスフィルタの特性を持ちます。第2項は2次系のローパスフィルタの伝達関数になっていますね。ちなみに、第1項を無視して、第2項のみの係数を考えますと、 $$ \begin{align} \frac{Y(s)}{X(s)}=\frac{\frac{K_{i}K_{t}}{J{m}}}{s^2+s\frac{B_{m}+K_{p}K_{t}}{J_{m}}+\frac{K_{i}K_{t}}{J{m}}}\\
\end{align} $$ 以下は2次系の伝達関数です。 $$ \begin{align} G(s)=\frac{\omega_{n}^2}{s^2+2\zeta\omega_{n}^2+\omega_{n}^2}\\
\end{align} $$ 係数を比較して、KpとKiを決定すると、$\omega_{n}$と$\zeta$を変化させて応答を自由に設計できます。 $$ \begin{align} K_{i}&=\frac{J_{m}}{K{t}}\omega_{n}^2\\
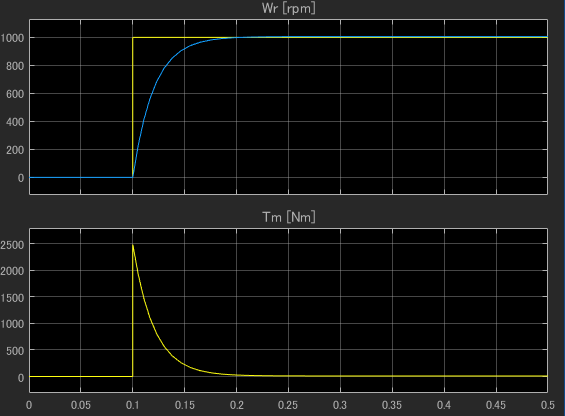
K_{p}&= \frac{2\zeta\omega_{n}^2J_{m}-B_{m}}{K_{t}} \end{align} $$ ただし、このようなゲイン設計は第1項が第2項に比べて小さく近似できる場合に限られます。 適当に以下のパラメータを入れて、ステップ応答を確認してみました。　

$\omega_{n}=5.0, \zeta=1.0, Kt=1.0[Nm/A], J_{m}=0.1 [kgm^2], B_{m}=0.0[Nm/(rad/s)]$

　波形をみると、ステップ入力後100msecで定常状態になっていますね。目標に対して2%以内に収まる2次系ローパスフィルタの整定時間は $$ T_{se} = \frac{\ln (0.02)}{\zeta\omega_{n}^2} $$

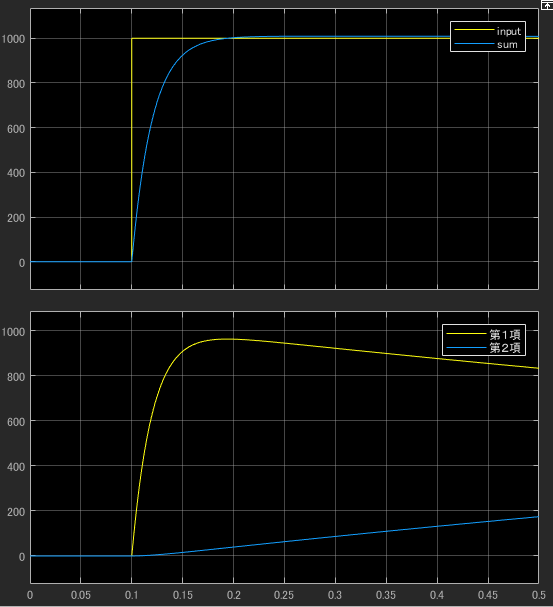
$\omega_{n} = 5.0, \zeta=1.0$なので、782.4 msecですね。ゲイン設計通りにはいっていないです。 確認のため、同じパラメータ条件で第1項と第2項のステップ応答を確認してみます。

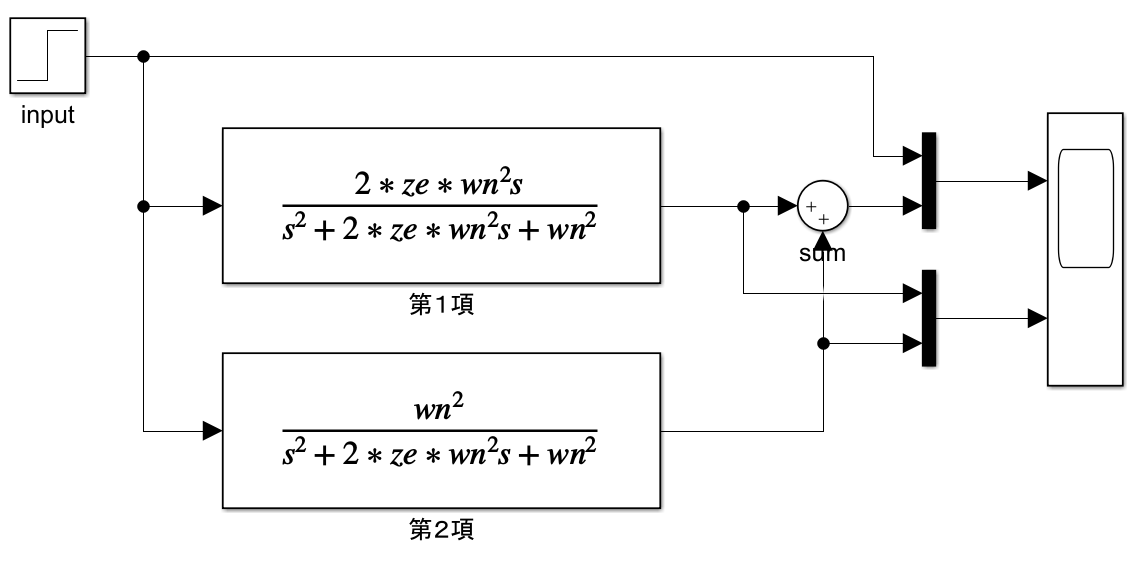
上の波形はモデルが同じなので、当然同様の応答ですね。下の波形より、第1項（バンドパスフィルタ）の立ち上がりが早いですね。 応答が早い理由は、第1項による影響であることがわかりました。

ILC制御による外乱トルク抑制効果

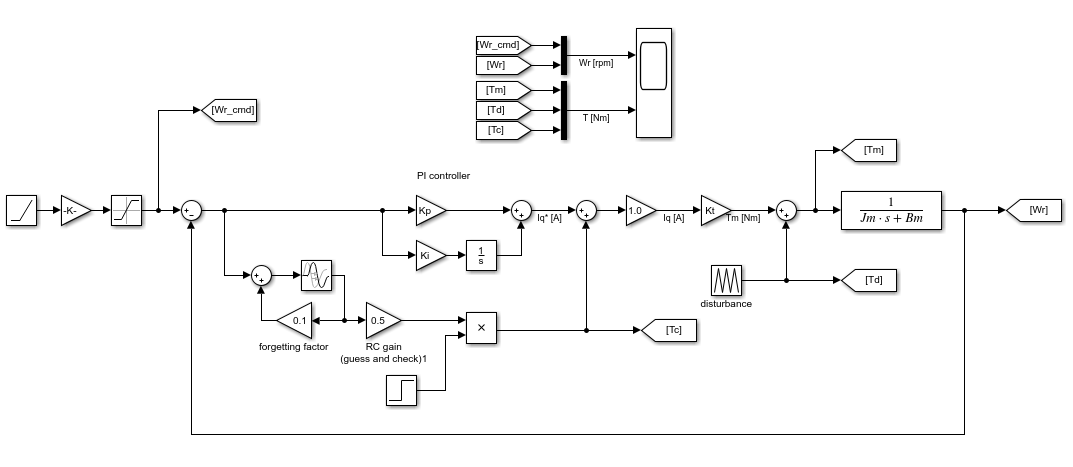
　先ほどの簡易モデルに、ILC制御器と、外乱トルクを入れてみました。 速度指令と速度フィードバックの偏差を入力し、その出力をq軸電流指令に フィードフォワードで補償してます。

図からわかるように、ILC制御器の忘却要素$\alpha=0.1$、$\Phi=1.0$、$\gamma=0.5$としました。なお、ILCの積分器の遅延要素は、外乱トルクの周期と同じになるように遅延ブロックを入れています。シミュレーションした結果が以下の図となります。

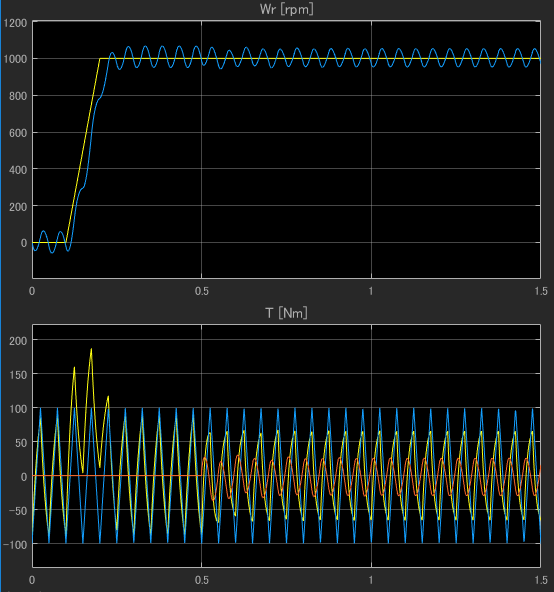
上波形の黄色い波形が、速度指令(Wr_cmd)となっており、0.2 [sec]で1000 rpmまで加速してます。青が実際の速度(Wr)で振動していますが、これは外乱トルク(Td)の影響です。下波形の青色が一定周期で与えられている外乱トルク(Td)です。黄色い波形はモータにかかっているトルクTmとなってます。オレンジの波形がILC制御器の出力であり、シミュレーション時間0.5 [sec]で有効となるように与えています。

0.5 sec後にモータのトルクTmの振動のピークが下がっていることが確認できます。（わかりずらい波形で申し訳ないです）

トルクの振動は少し弱くなりましたが、速度の振動はあまり変化ないですね… イナーシャが小さいから？何か、考え方かシミュレーションが間違っているかもしれないです？

本ページでは、制御器のゲインを適当に入れましたが、モデルを解いて不安定にならないようにゲインをしっかり設計する文献などもあります。（参考文献(2)）

【参考文献】
(1) Institute of Electrical Engineering, Chinese Academy of Sciences, China,
A Simpler and More Efficient Iterative Learning Controller for PMSM Torque Ripple Reduction

(2) Torque Ripple Minimization of PMSM Using Parameter Optimization Based Iterative Learning Control