Kaggleの過去コンペSantander Customer Satisfaction
Kaggleの過去コンペSantander Customer Satisfactionの勉強の記録です。
以下参考にしたKernelです。
概要
サンタンデール銀行の顧客が銀行のサービスに満足、不満足なのかを予測するコンペです。
サービスに満足しない顧客は、とくに不満を言うことなく銀行を離れていくため、事前に対策を打って顧客離れを防ぐことが目的のようです。
本コンペは多くの匿名データより、どのような顧客が銀行のサービスに不満を持っているのか予測して精度を競います。
全部で371種類の特徴量があり、そのうちの’TARGET’カラムを予測します。1であれば不満のある顧客で、0なら満足している顧客です。予測結果はAUCで評価します。
EDA・特徴エンジニアリング
モデルを読込みます。
train = pd.read_csv("../input/train.csv")
test = pd.read_csv("../input/test.csv")分散0(すべて同じ値)の列を削除します。また、列同士で同じ値の列も削除します。
# remove constant columns (std = 0)
remove = []
for col in train.columns:
if train[col].std() == 0:
remove.append(col)
train.drop(remove, axis=1, inplace=True)
test.drop(remove, axis=1, inplace=True)
# remove duplicated columns
remove = []
cols = train.columns
for i in range(len(cols)-1):
v = train[cols[i]].values
for j in range(i+1,len(cols)):
if np.array_equal(v,train[cols[j]].values):
remove.append(cols[j])
train.drop(remove, axis=1, inplace=True)
test.drop(remove, axis=1, inplace=True)列を確認してみます。
train.head(8).iloc[:,:8]| | ID | var3 | var15 | imp_ent_var16_ult1 | imp_op_var39_comer_ult1 | imp_op_var39_comer_ult3 | imp_op_var40_comer_ult1 | imp_op_var40_comer_ult3 |
|----+------+--------+---------+----------------------+---------------------------+---------------------------+---------------------------+---------------------------|
| 0 | 1 | 2 | 23 | 0 | 0 | 0 | 0 | 0 |
| 1 | 3 | 2 | 34 | 0 | 0 | 0 | 0 | 0 |
| 2 | 4 | 2 | 23 | 0 | 0 | 0 | 0 | 0 |
| 3 | 8 | 2 | 37 | 0 | 195 | 195 | 0 | 0 |
| 4 | 10 | 2 | 39 | 0 | 0 | 0 | 0 | 0 |
| 5 | 13 | 2 | 23 | 0 | 0 | 0 | 0 | 0 |
| 6 | 14 | 2 | 27 | 0 | 0 | 0 | 0 | 0 |
| 7 | 18 | 2 | 26 | 0 | 0 | 0 | 0 | 0 |var~と名前のついた変数がありますね。コンペのDataのページをみても変数の説明がなく、何を表しているかわかりません。
有志達の分析により、ある程度変数の意味がわかっており、例えば以下のようなものがあります。
- var3: 国籍
- var15: 顧客の年齢
- var38: 担保の価値
- num_var4: 銀行の商品の数
以下のVrije Universiteit Amsterdam(アムステルダム自由大学)のレポート? が参考になります。
https://beta.vu.nl/nl/Images/werkstuk-elsen_tcm235-865964.pdf
test_idにtestデータのIDを保存して、trainとtestのIDの列を除去します。
test_id = test.ID
test = test.drop(["ID"],axis=1)
X = train.drop(["TARGET","ID"],axis=1)
y = train.TARGET.valuesPCAで第1~第3主成分ベクトルを抽出します。各主成分ベクトルにデータをプロジェクションして 新しい特徴量として列に追加します。
features = train.columns[1:-1] # remove ID, TARGET
pca = PCA(n_components=3)
x_train_projected = pca.fit_transform(normalize(train[features], axis=0))
x_test_projected = pca.transform(normalize(test[features], axis=0))
X.insert(1, 'PCAOne', x_train_projected[:, 0])
X.insert(1, 'PCATwo', x_train_projected[:, 1])
X.insert(1, 'PCAThree', x_train_projected[:, 2])
test.insert(1, 'PCAOne', x_test_projected[:, 0])
test.insert(1, 'PCATwo', x_test_projected[:, 1])
test.insert(1, 'PCAThree', x_test_projected[:, 2])sklearnのnormalizeは各列ごとにL2ノルムで正規化してます。 (2乗和を1としている)。オプションでUnit Norm(L1ノルム)の正規化などもできます。 PCAの各成分の寄与率は
print(pca.explained_variance_ratio_)
>> [0.07773946 0.05429553 0.04157066]
print(sum(pca.explained_variance_ratio_))
>> 0.173605541480345273つ合わせて17%くらいになりました。
次に特徴量の重要度を調査してみます。ExtraTreesClassifierを利用して調べることができます。 これはExtremely Randomized Treesを使っており、 あまり詳しく理解していませんが、木を構築していく際に閾値をランダムに選ぶことで木同士の独立性が高くなるようです。 ランダムフォレストに対して特徴抽出に向いていますが、モデルの誤差は下がる傾向にあるようです(ただし過学習しにくい)
以下にExtremely Randomized Treesの文献があります。
https://link.springer.com/article/10.1007/s10994-006-6226-1
clf = ExtraTreesClassifier(random_state=405,bootstrap =True,class_weight = "balanced")
selector = clf.fit(normalize(X), y)
# plot most important features
fig = plt.figure(facecolor = 'white')
feat_imp = pd.Series(clf.feature_importances_, index = X.columns.values).sort_values(ascending=False)
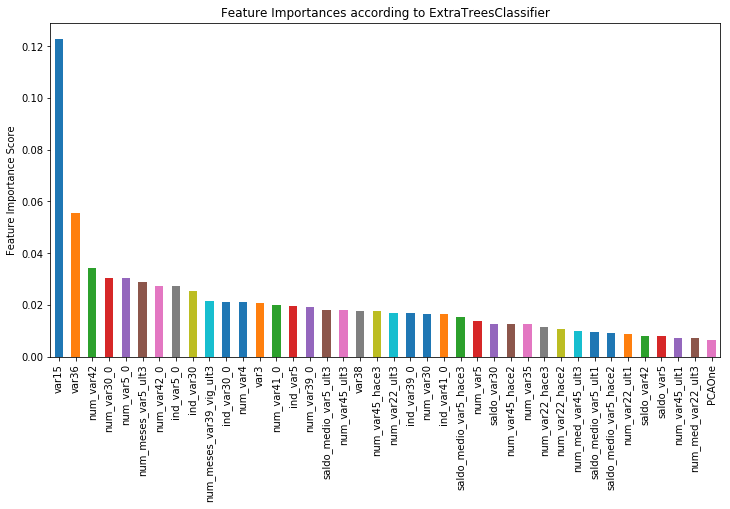
feat_imp[:40].plot(kind='bar', title='Feature Importances according to ExtraTreesClassifier', figsize=(12, 8))
plt.ylabel('Feature Importance Score')
plt.subplots_adjust(bottom=0.3)
plt.show()
fs = SelectFromModel(selector, prefit=True)
X = fs.transform(X)
test = fs.transform(test)var15, var36の割合が大きいですね。上記コードでSelectFromModelを使って、ExtraTreesClassifierで抽出した重要度に基づいて特徴量の
絞り込みをしています。thresholdを指定して閾値を指定できますが、何も指定しない場合はmeanが使われます。
モデル構築
xgboostでモデルをつくります。
m2_xgb = xgb.XGBClassifier(missing=np.nan, max_depth=6,
n_estimators=320, learning_rate=0.03, nthread=4, subsample=0.95,
colsample_bytree=0.85, seed=3242)
metLearn = CalibratedClassifierCV(m2_xgb, method='isotonic', cv=10)
metLearn.fit(X,y)CalibratedClassifierCVは予測値が2値分類の確率を示すように校正をするために用いられます。(Probability calibration)。ロジスティック回帰の場合、校正しなくても予測値が確率値を示しますが、ランダムフォレスト、ナイーブベイズ、SVMなどはバイアスを持った 値となるようです。
CalibratedClassifierCVの引数でcv=10とありますが、これは10回の交差検証に対しての出力の平均値を確率値とするようです。 交差検証は次のクラスでデータの分割が行われます(StratifiedKFold)
以下文献が参考になると思います
Predicting good probabilities with supervised learning by Caruana et al.
スコア出力
probs = metLearn.predict_proba(test)
submission = pd.DataFrame({"ID":test_id, "TARGET": probs[:,1]})
submission.to_csv("submission.csv", index=False)提出した結果、スコアは「0.837914」でした。5200人チームのうち、2800番目くらいの順位ですね。
上位50%にも入っていないです。(kernelにある手法そのままなので当然ですが)。
なお、本コンペは、期限が切れているため、submitしてもleaderboardには名前が載りません。
トップ3のアプローチ
次のDiscussion(3rd place solution)で 3位入賞の8人チームのメンバーがコメントしており、コンペでのアプローチをgithubにアップしているとコメントしてます。こちらがgihubのページです。最後は各人のモデルをブレンドして最終結果を出力しています。
利用しているモデルをみてみると以下のものがあります。
- Neural Network (NN)
- Ada-boosted Trees
- KNN
- Regulalized Greedy Forest (RGF)
- Follow The Regularized Leader- Proximal (FTRL-Proximal)
まだまだ私の知らないアルゴリズムがあります…また調べておこう。