はじめに
matlab, simulinkを使ってシンプルなローパスフィルタについてシミュレーションします。
連続モデルのローパスフィルタ
ローパスフィルタの伝達関数は以下のように記述できます。
$$
\begin{align}
\frac{Y(s)}{X(s)} &= \frac{1}{T_{c}s+1}\\
&= \frac{\omega_{c}}{s+\omega_{c}}
\end{align}
$$
$\omega_{c}$ は遮断周波数 [rad/sec]であり、$T_{c}$ は時定数 [sec]です。 $\omega_{c} = \frac{1}{T_{c}}$ となります。 ここで、伝達関数を以下のように変形してみましょう。
$$
\begin{align}
Y(s){(T_{c}s+1)} &= X(s)\\
Y(s) &= \frac{X(s)-Y(s)}{T_{c}s}
\end{align}
$$
すなわち、入力$X(s)$から出力$Y(s)$を減算して、${T_{c}}$で除算して、積分した結果となります。これは、元の伝達関数と同じであるため、入力に対して同じ応答になるはずです。
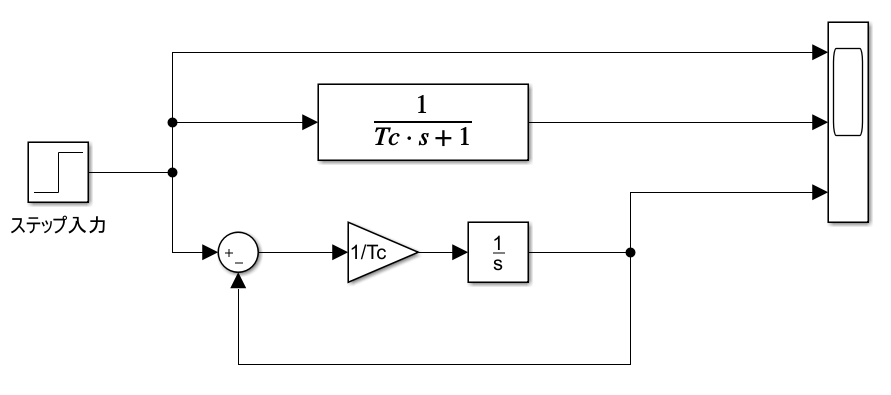
動作を確認するため、simulinkで以下ブロック図を作成しました。
Tc = 0.1 [sec]とし、ステップをシミュレーション時間0.1 [sec]で入力した時の応答波形をスコープで示します。以下、スコープの表示です。
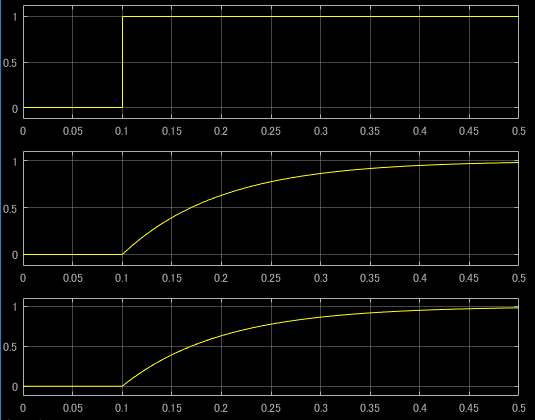
スコープ2番目と3番目の応答が同じであることが確認できますね。また、Tc=0.1 [sec]であるため、ステップ入力してから、0.1 [sec]後に 1.0の63.2 [%] である0.632になっています。